![]()
I’-m just finishing writing a new research paper whose goal is to come up with a better measure and understanding of the lagged effect of monetary policy on the economy. One of my claims is that the public’-s expectations of what the Fed is going to do next play a key role in that process. In this, the first of several posts based on that paper, I describe some of the properties I’-ve found for fed funds futures prices as predictors of subsequent Fed policy changes.
The primary policy tool of the U.S. Federal Reserve is manipulation of the federal funds rate, an overnight interest rate on interbank loans that is quite sensitive to the total quantity of reserve deposits that are created by the Fed. The Chicago Board of Trade offers a futures contract whose payoff is based on the average value for the effective fed funds rate over all of the calendar days of a specified month.If this were a pure forward contract, no money would change hands until the first-of-month settlement day. The actual futures contracts are a little more complicated, since the exchange will require you to commit collateral to prove you can honor the contract, and these margin requirements will increase if the market moves against you. However, a recent paper by Monika Piazzesi and Eric Swanson demonstrates that the impact of these margin calculations on the value of the contracts should be quite small, and I will discuss here the simpler case of how to evaluate a pure forward contract.
Consider first how a contract that specified a 5.25% value for the current month’-s fed funds rate would be valued at the start of the last day of the month (the day before settlement). If the actual rate turns out to be lower than 5.25%, the next day the seller of the contract will have to compensate the buyer for the difference (paying $41.67 per basis point in the standard contract). If you were the buyer of the contract, this would for you be a pure profit. The primary consideration that might prevent you from taking this bet is a concern that perhaps the rate would end up above 5.25%, in which case you’-ll owe money. If speculators are risk neutral, the contract price will be bid up or down to the point at which its implied interest rate just equals traders’- expectations of what the settlement rate will turn out to be.
On the next-to-last day of the month, similar logic would again imply that the price reflects the market expectation at that time. New information could well come in after this, causing the price to move up or down before settlement. But if it were possible to anticipate, say, a price increase between the penultimate and last day of the month, there is a pure profit opportunity from buying on October 30 and selling on October 31. A statistical principle known as the Law of Iterated Expectations implies that the October 30 price should not only equal the expected settlement value, it should also equal the expected October 31 price. As time goes on and new information comes in, of course we know that the price is likely to change. But none of us can predict the direction. In other words, this simple theory suggests that the futures price should follow a martingale, in which the best forecast of where the price is going to be tomorrow is always just today’-s price.In my statistical analysis I looked at daily changes in the interest rate implied by the current month’-s fed funds contract (denoted f1d), the following month’-s contract (f2d), and the month after that (f3d)- for example, for d = October 31 we could consider the change in the October contract (f1d), the November contract (f2d), or the December contract (f3d). The graph below plots daily changes in the interest rate implied by the current month contract from October 1988 through June 2006.
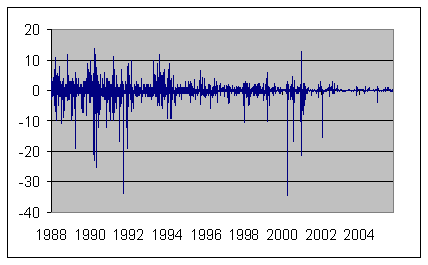 |
On average, the values of f1d, f2d, and f3d all turn out to be negative over this sample period, with t-statistics around -4. This represents strong evidence against the martingale hypothesis, and some researchers have interpreted this bias as evidence of some kind of average risk or hedging premium reflected in the futures prices.
However, if you look at the graph above, you will see that it is a pretty wild series. Forty-six percent of the observations are identically zero, while 25 observations exceed 5 standard deviations. The variance is considerably larger at the beginning of the sample or the start of a month, with the volatility appearing in clusters and particularly on days of major monetary policy announcements. If one models all these volatility dynamics and departures from a Gaussian distribution, the maximum likelihood estimate of the population mean of f1d, f2d, or f3d all turn out to be positive rather than negative, and far from statistically significant. The sample median of all three series is also exactly zero. I therefore see the nonzero sample mean not as an indication of bias on the part of futures markets, but rather as reflecting the fact that there were a few big moves down in interest rates over this period
that caught traders by surprise.
I also looked for whether changes could be predicted on the basis of lagged changes, by regressing fid on a constant and five of its own lagged changes. OLS coefficient estimates along with their 95% confidence intervals are shown below.
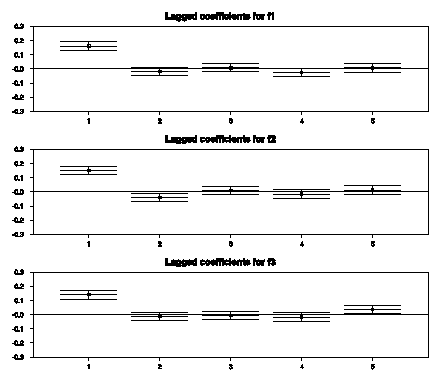 |
The first lag is always highly statistically significant. Its value, however, is only around 0.15, which gives the regression an R2 of less than 0.03 and essentially zero predictability looking more than one day ahead. It is quite likely that this very modest degree of predictability could be attributed to measurement error in resolving daily bid-ask factors rather than systematic errors or risk factors in futures markets.
The paper by Piazzesi and Swanson mentioned above documents some predictability using monthly data of longer-horizon fed funds futures prices based on a number of interest rate spreads. However, consistent with their findings, I find these spreads do not predict the daily movements in the prices associated with the near-term fed funds futures contracts that I am studying, as summarized in the table below:
| Explanatory variable | Dependent variable | ||
|---|---|---|---|
| xd-1-1 | f1d | f2d | f3d |
| 10-year minus 5-year Treasury spread | 0.058 (0.086) | -0.036 (0.117) | -0.070 (0.138) |
| 5-year minus 2-year Treasury spread | -0.009 (0.058) | -0.085 (0.079) | -0.126 (0.093) |
| 2-year minus 1-year Treasury spread | -0.072 (0.112) | -0.136 (0.153) | -0.172 (0.181) |
| 1-year minus 6-month Treasury spread | 0.006 (0.173) | 0.302 (0.236) | 0.439 (0.279) |
| Baa minus 10-year Treasury spread | -0.035 (0.058) | -0.126 (0.079) | -0.184* (0.094) |
| 12-month job growth (revised data) | 0.017 (0.023) | 0.089** (0.031) | 0.125** (0.036) |
| 12-month job growth (real-time data) | 0.016 (0.024) | 0.093** (0.033) | 0.121** (0.039) |
I also replicate with these data Piazzesi and Swanson’-s observation that employment growth helps predict futures prices, though again for my data the R2 is only 2%, and the results I will describe in my next post turn out to be insensitive to whether one includes this conditioning variable. Overall, I conclude that although these data do not appear to follow an exact martingale, that is really an excellent approximation to their behavior.
A separate question from whether changes in futures prices are possible to predict is the question of how far in advance they give a useful estimate. One standard of comparison is the mean squared error, or the average squared difference between the implied futures forecast at a given date and what the actual fed funds rate turns out to be. A benchmark for comparison is the assumption that the fed funds rate itself follows a martingale, so that one’-s forecast for the future value of the fed funds rate is always its current value. Such “-no-change”- forecasts have often proven to be very difficult to beat out-of-sample with financial data. The table below shows that, if you simply predicted that the fed funds rate isn’-t going to change, you’-d have a mean squared error of 389 basis points (that is, a standard deviation of about 20 basis points or 0.2%) predicting one month ahead and 2,522 basis points (50 basis-point standard deviation) predicting 3-months ahead. For comparison, the MSEs of the futures-derived forecasts are only a third as large.
| Forecast horizon | No-change MSE | Futures MSE | Percent MSE improvement | Futures MAE |
|---|---|---|---|---|
| 1 month ahead | 389 | 128 | 67% | 6.90 |
| 2 months ahead | 1248 | 392 | 69% | 12.76 |
| 3 months ahead | 2522 | 914 | 64% | 20.03 |
Futures prices have become even better predictors over the last three years, with an incredible 97% improvement over the “-no-change”- forecast:
| Forecast horizon | No-change MSE | Futures MSE | Percent MSE improvement | Futures MAE |
|---|---|---|---|---|
| 1 month ahead | 183 | 5 | 97% | 1.50 |
| 2 months ahead | 665 | 19 | 97% | 3.18 |
| 3 months ahead | 1484 | 48 | 97% | 5.40 |
The moral is, if you think the fed funds rate is going to do something over the next few months that differs from what is predicted by the futures prices, then think again.
And what the futures prices say right now is, no change in December.

